Making Sense Of "2 5" - Your Friendly Math Guide
Have you ever looked at a number combination like "2 5" and wondered what it could possibly mean? Maybe it's a measurement, a part of something bigger, or even a way to show how many times you multiply a number by itself. It's actually kind of interesting how a simple pair of digits can tell so many different stories in the world of numbers.
So, it's almost like our everyday lives are filled with little puzzles, and sometimes, those puzzles involve numbers. Whether you're trying to figure out how much of a recipe to use or just checking a calculation for something you're building, getting a good grasp on how numbers work can really make things easier. This is where handy math tools come into play, offering a bit of help when you need to sort out things like fractions, powers, or even how long something is.
You know, for instance, these tools are pretty good at taking something that might seem a little tricky, like figuring out what "2 to the power of 5" means, and making it quite clear. Or, perhaps, you're just looking to turn "2/5" into a simple decimal. Whatever your number challenge happens to be, there are ways to get a handle on it, and we're here to talk about how these helpers can make numbers feel a lot less intimidating.
Table of Contents
- Getting a Handle on Numbers - What Does 2 5 Mean?
- Making Sense of Fractions - Like 2/5, For Instance
- Figuring Out Powers - What's 2 to the Power of 5?
- How Do Calculators Help with Everyday Math?
- Tackling Longer Problems - Like Those Algebra Bits
- Converting Measures - How Long is 2.5 Meters in Other Units?
- Following the Rules - Order of Operations for 2 5 Problems
- Getting a Better Look - Visualizing Math with 2 5
Getting a Handle on Numbers - What Does 2 5 Mean?
When you see "2 5," it could, you know, point to a few different ideas depending on the situation. It might be talking about a decimal number, like 2.5, which is two and a half. Or, in some respects, it could be showing a fraction, like 2/5, which is two parts out of five equal parts. Then there's the idea of "2 to the power of 5," which is a way of saying you multiply the number 2 by itself five times. Each of these ways of looking at "2 5" has its own set of things you might want to figure out.
So, whether you're trying to work with portions of something, figure out a measurement, or calculate how many times a number grows, having good tools at your side makes a real difference. Actually, these tools are built to help you draw things out, scan what you've written, get answers to problems, and learn a bit more along the way. They take the kind of number questions that might make you scratch your head and give you a way to see them through.
For instance, if you're dealing with long number sentences or just want to sketch out your thinking, these helpers can let you do that, even when you hold your device sideways. They can also show you how to get to the answer for problems and, you know, give you a simple explanation for what different number ideas mean. It’s pretty much about making math less of a mystery and more of a clear path to the answer.
Making Sense of Fractions - Like 2/5, For Instance
A fraction, basically, is a number that shows a piece of a whole thing. It’s like when you cut a pie into equal slices and take some of them. It has two main parts: the top number, which is called the numerator, and the bottom number, which is called the denominator. The top number, the numerator, tells you how many pieces you have, and the bottom number, the denominator, tells you how many equal pieces make up the whole thing. So, for "2 5" as 2/5, you have two pieces out of a total of five pieces.
You know, turning a fraction like 2/5 into a decimal is actually quite straightforward. All you do is take the top number and divide it by the bottom number. So, for 2/5, you would do 2 divided by 5, which gives you 0.4. That's, you know, honestly, all there is to that particular bit of figuring. It's a simple move that makes fractions easier to work with in some situations.
Then there are tools that let you work with fractions in all sorts of ways. You can, for example, add them together, take one away from another, multiply them, or even divide them. These helpers make sure you get the right outcome, especially when you're trying to combine or separate different parts of a whole. It’s quite useful for recipes or anything else that involves splitting things up.
Figuring Out Powers - What's 2 to the Power of 5?
When we talk about "power" or "exponents," we're really just talking about how many times a number gets multiplied by itself. So, for instance, if you hear "2 to the power of 3," that means you take the number 2 and multiply it by itself three times: 2 multiplied by 2, and then that result multiplied by 2 again. It's a quick way of writing down repeated multiplication. So, for "2 5" as 2 to the power of 5, you're doing 2 multiplied by itself five times.
To figure out "2 to the power of 5," you would do this: 2 times 2 equals 4. Then 4 times 2 equals 8. Then 8 times 2 equals 16. And finally, 16 times 2 equals 32. So, 2 to the power of 5 is 32. It’s just a shorthand for a series of multiplications. You know, these kinds of calculations can get pretty big pretty fast, which is where special tools come in handy.
There are tools that can figure out the power of numbers, even if the base number is quite large or if the number you're raising it to is also big, like exponents less than 2000. They can even handle negative exponents and numbers that aren't whole. This is pretty useful, honestly, when you're dealing with numbers that would take a long time to multiply out by hand. They just make it quick and simple to get the answer for things like "2 5" in this context.
How Do Calculators Help with Everyday Math?
Well, you know, at their most basic, calculators are there to do simple number work for us. They can add numbers together, take one number away from another, multiply numbers, and divide them. These are the kinds of calculations we do all the time, whether we're figuring out a grocery bill or just splitting something with friends. It's really just a quick way to get those everyday number tasks done without a lot of fuss.
Then there are the more advanced types, sometimes called scientific calculators. These go beyond just the simple stuff. They can help you with percentages, which are pretty useful for sales or tips, and they can also deal with fractions, as we talked about earlier. They handle things like exponential functions, which are those "power of" calculations we just discussed, and logarithms, which are kind of the opposite of exponents. They also help with trigonometry, which deals with angles and shapes, and statistics, which is about making sense of groups of numbers. It’s pretty comprehensive, actually, for a small device.
And, you know, a really nice thing about these tools is how they can help you check your school work. It’s an easy way to see if you got the right answer to a problem you've been working on. You can put in your problem, and it will give you the answer, helping you feel more sure about what you've done. It's like having a helpful friend who's really good with numbers right there with you.
Tackling Longer Problems - Like Those Algebra Bits
Algebra, you know, is a part of math where you often work with letters and symbols that stand for numbers. It's about finding out what those unknown numbers are. Tools that help with algebra can do things like expand expressions, which means taking something like (x + 2)(x + 3) and multiplying it all out. They can also factor expressions, which is the opposite – taking a long expression and putting it back into a simpler, multiplied form. It's pretty handy for making sense of those kinds of number sentences.
These helpers also let you get answers to long number sentences, and they even show you how to get there, step by step. They can explain why a certain move matters and how each step brings you closer to the final answer. This is really useful, basically, for learning how to do these kinds of problems on your own. It's not just about getting the answer; it's about seeing the process, too.
Furthermore, these tools are pretty good at figuring out the roots of polynomials, which are special kinds of algebraic expressions, and solving systems of equations, where you have several number sentences with several unknowns that all need to be true at the same time. They can even draw pictures of these number ideas, which helps you see what's happening. You know, it's a way to get a clearer picture of the number world.
Converting Measures - How Long is 2.5 Meters in Other Units?
When you hear "2 5" as 2.5 meters, it's a way of talking about length. Sometimes, you might need to know how long that is in a different way, like in feet. It's quite common to need to change from one unit of measurement to another, especially if you're looking at plans from a different country or just trying to get a sense of size in a more familiar way. So, you know, knowing how to convert 2.5 meters to feet is a practical skill.
There are simple tools that let you do this kind of conversion really easily. You just put in the 2.5 meters, and it tells you what that is in feet. It saves you the trouble of having to remember conversion factors or doing the multiplication yourself. This is pretty much about making everyday measurements straightforward and easy to understand, especially when you're dealing with different systems of length or height.
For example, if you're trying to figure out how tall something is, and it's given in meters, but you think in feet, a conversion tool is very helpful. It just takes the number you have and gives you the equivalent in the unit you prefer. It's a small thing, perhaps, but it makes a big difference in how easily you can use information that comes in different measurement forms.
Following the Rules - Order of Operations for 2 5 Problems
When you have a number sentence with lots of different operations, like adding, subtracting, multiplying, and dividing, you can't just do them in any order. There's a specific set of rules to follow to make sure everyone gets the same answer. This set of rules is often remembered by names like PEMDAS, BEDMAS, BODMAS, or GEMDAS. Each letter stands for a step you take: Parentheses/Brackets first, then Exponents/Orders, then Multiplication and Division (from left to right), and finally Addition and Subtraction (from left to right). So, you know, it’s a way to keep things consistent.
This order really matters because if you do the operations in a different sequence, you'll end up with a different answer. For example, if you have 2 + 3 * 4, and you add 2 and 3 first, you get 5 * 4 = 20. But if you follow the rules and multiply 3 and 4 first, you get 2 + 12 = 14. See how different the answers are? So, actually, sticking to the order is pretty important for getting the right outcome for problems that might involve "2 5" in a longer expression.
There are tools that are built to automatically follow these rules. You can type in your whole number sentence, and the tool will figure out the answer by doing the operations in the correct order. This is really useful because it takes the guesswork out of it and helps you avoid common mistakes. It's like having a little expert inside your calculator who always remembers the right way to do things.
Getting a Better Look - Visualizing Math with 2 5
Sometimes, just looking at numbers isn't enough to really get what's going on. That's where graphing tools come in. They let you see math, literally. You can put in a number sentence, and it will draw a picture of it on a graph. This is pretty cool because it helps you understand how numbers relate to each other and how they change. You know, it's a visual way to get a grasp of things that might seem abstract.
These graphing helpers can do a lot more than just draw simple lines. They let you plot individual points, which is useful for seeing where specific numbers sit. You can also add "sliders," which are like little controls that let you change a number in your equation and see how the graph changes in real-time. You can even make the graphs move, which is called animating them, showing how things shift over time or with different values. It’s pretty dynamic, honestly.
For instance, if you're working with something like "2 5" in an equation, seeing how that equation behaves when you change other numbers around it can give you a much deeper sense of what's happening. It's about turning numbers into shapes and movements, which can make learning about them a lot more interesting and clear. It’s a great way to explore how different number ideas connect and interact with each other.

Comparing fractions - free lesson with a video
![What is 2/5 as a decimal? [Solved]](https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/2-5-as-a-decimal-is-0-4-1622010496.png)
What is 2/5 as a decimal? [Solved]
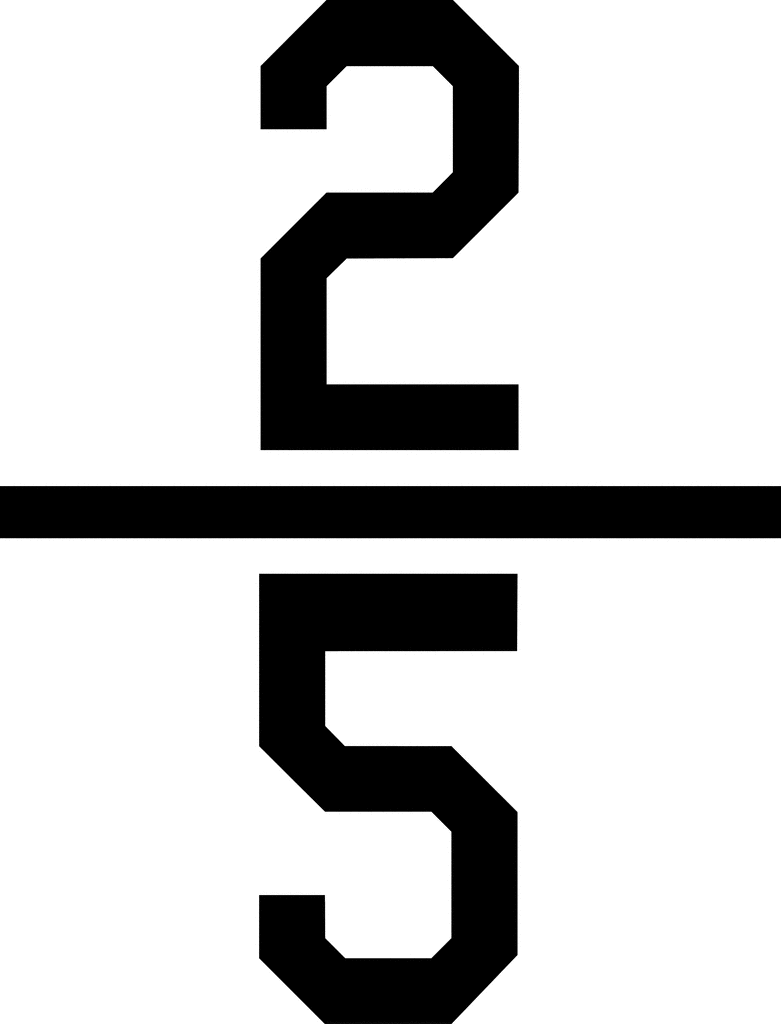
Numerical fraction 2/5 | ClipArt ETC